Non-Technical Definition:
The minimum sum of a graph is the minimum, over all labelings of the vertices with distinct integers, of the sum of differences between all vertices connected by edges.
Technical Definition:
For a given graph G=(V,E), consider labelings that assign each vertex a distinct number from 1 to n where |V|=n. For each labeling f, the linear sum s(f) of f is the sum of |f(u)-f(v)| for all (u,v) in E. The linear sum of the graph G is the minimum value of s(f) where f ranges over all labelings of G. In other words, s(G) = min {s(f) : f is a labeling of G} [1]
Explanations:
The minimum sum problem is much like the bandwidth problem. The bandwidth problem deals with minimizing the maximum stretch over all of the edges. The mimimum sum problem deals with mimimizing the total sum of all the stretches over all the edges in a graph. In order to do that, the stretch over each edge needs to be minimized, which in a way makes the bandwidth problem a special case of the minimum sum problem.
For example:

However this is not always the case, minimizing bandwidth does not always minmize the sum over all edges.
For example:
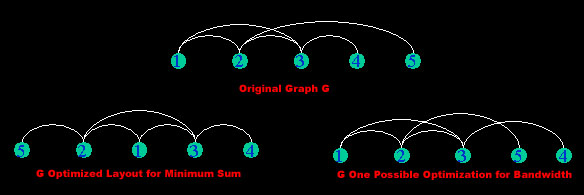
However, the bandwidth solution is still a good approximation of the minimum sum problem. Whatever the resulting graph the bandwidth solution produces gives a nice upper bound for the minimum sum problem. The upper bound is that the sum of the graph resulting from the bandwidth solution, must be greater than or equal to the optimal graph for the minimum sum.
Observation 1:Thus s(f) <= |f(u)-f(v)| for all (u,v) in E, where E is the edge set in the graph produced by the optimal bandwidth solution.
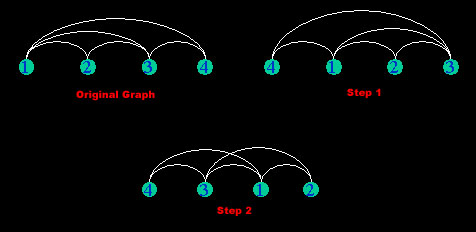
|f(1)-f(2)| + |f(2)-f(3)| + |f(3)-f(4)| + |f(1)-f(3)| + |f(1)-f(4)| = 1 + 1 + 1 + 2 + 3 = 8.
After moving vertex 4 all the way to the left of the graph, the sum is still 8.
|f(1)-f(2)| + |f(2)-f(3)| + |f(3)-f(4)| + |f(1)-f(3)| + |f(1)-f(4)| = 1 + 1 + 3 + 2 + 1 = 8.
Thus we keep going to find a minimum sum. After step 2, the sum is 7.
|f(1)-f(2)| + |f(2)-f(3)| + |f(3)-f(4)| + |f(1)-f(3)| + |f(1)-f(4)| = 1 + 2 + 1 + 1 + 2 = 7.
This is the best possible arrangement of the graph and we get 7 as the minimum sum of the graph.
Observation 2: For a set of vertices nx...ny, if nx and ny are connected by an edge and every vertex between is connected by an edge of length one to the vertices adjacent to it, then there is no furthur optimization possible on this set of vertices.
*In the example above, this applies to the vertex sets [4,3,1] and [3,1,2] of the final graph.
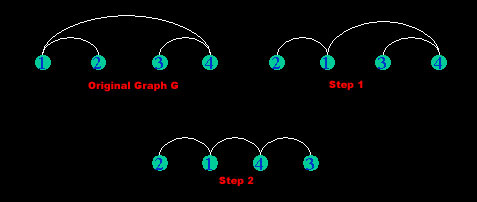
|f(1)-f(2)| + |f(3)-f(4)| + |f(1)-f(4)| = 1 + 1 + 3 = 5.
After moving vertex 2 all the way to the left of the graph, the sum reduces to 4.
|f(1)-f(2)| + |f(3)-f(4)| + |f(1)-f(4)| = 1 + 1 + 2 = 4.
Thus we keep going to find a minimum sum. After step 2, the sum is 3.
|f(1)-f(2)| + |f(3)-f(4)| + |f(1)-f(4)| = 1 + 1 + 1 = 3.
This is the best possible arrangement of the graph because all edges have length 1 and we get 3 as the minimum sum of the graph.
Observation 3: Anytime the graph has edges where |f(x) - f(y)| = 1 for all x,y vertex pairs, then the minimum sum is n - 1 where n is the number of vertices. This is also the best possible layout since no edge length can be reduced below one.
Since the bandwidth approximation gives the minimum sum in certain cases and produces an upper bound for finding the minimum sum in a graph, we can just use the bandwidth heuristic in order to give us a layout for a possible solution to the minimum sum problem. In Skienna's "Algorithm Design Manual", he states that the solution to the bandwidth problem can be done in O(nb^2) time on matrices with bandwidth b. Thus, using the bandwidth heuristic, it is also possible to find a layout for the minimum sum in O(nb^2) time, since the actual calculation of the minimum sum after finding a layout is linear. In many cases this will work, but in others, the layout generated from the solution to the bandwidth problem will only give a good approximation of the answer for the minimum sum. If it is not the optimal layout, then the minimum sum is either equal to or less than the sum obtained from the layout produced by the bandwidth result. Either way, it is a good approximation for the minimum sum.
Heuristic 2:
The second heuristic deals with going through each permutation possible for the layout of the graph. In this way we are sure to find the absolute minimum sum because it tests all possiblities. However, there are a couple of stopping conditions that might allow the algorithm to complete in less than O(n!) time on n vertices. By observation 2 and 3 explained above, the algorithm will have found the optimal layout for the minimum sum and thus the algorithm can terminate and return the answer to the minimum sum problem for the graph given to it. Below is psuedo code for this heuristic.
/* Store graph into a vector by representing it with lists
of vertices connected to others by edges according to their
labels. For example, the first element of the vector would
represent vertex 0 and would hold a vector whose elements
represent all of the other vertices that are connected to it
by edges. The second would represent vertex 1, etc. Then
generate a layout and calculate its sum. If the layout
or sum meets one of the stopping conditions, then return
the result. Otherwise continue in the same way with
a new layout until either a stopping condition is reached
or every possible permutation of the layout was used.*/
public class MinimumSum {
public vertices = new Vector();
public layout = new Vector();
/* Initialize a global variable which will hold the smallest sum
calculated so far */
public int min_sum = 0;
/* Initialize a global variable which will hold the layout that
gave the smallest sum so far */
public Vector min_sum_layout = new Vector();
/* Initialize a global boolean variable which will be set to
true if the minimum sum is found */
public boolean min_sum_found = false;
public static void main(String argv[]) {
// Represent graph numerically with vector's
for (i = 0; i < number_of_vertices; i++) {
/* Create a vector to represent the vertex i and add it
to the vertices vector*/
vertices.addElement( new Vector() );
for ( j = 0; j < number_of_vertices; j++ ) {
/* If vertex i is connected to vertex j, add that vertex
to i's list which represents all vertices connected to
it by and edge. */
if ( vertex_at_j_connected_to_vertex_i ) {
// Add the vertex j that is connected to i.
(vertices.lastElement()).addElement(new Integer(j))
}
}
}
/* Go through each permutation of the vertices to find
best possible layout.*/
while ( (layout = getNextPermutation()) != null
&& min_sum_found == false) {
/* Set the minimum sum to the sum calculated from the new
layout and save the layout which gave this new
minimum sum */
if ( calculate_sum( layout ) < min_sum || min_sum == 0) {
min_sum = calculate_sum( layout ); // save minimum sum
min_sum_layout = layout; // save layout
}
/* As stated in Observation 3, when the sum is the number of
vertices - 1, then the best possible layout is found and
there is no need to keep trying more permutations.
Also if observation 2 is found to be true, the best
possible layout will have been found and the algorithm
can be terminated. These are the stopping conditions.*/
if ( min_sum = #_of_vertices_in_graph - 1
|| check_observation_2(layout) == true) {
min_sum_found = true;
}
}
// Returns the value of the minimum sum found for the graph.
return min_sum;
}
// Pseudo Functions to help calculate the minimum sum
public Vector getNextPermutation() {
/* function will return the next possible permutation in a vector.
It will return null if all permutations have been exhausted.
The function starts with the permutation 1,2,3...n and works
from there.*/
}
public int calculate_sum(Vector permutation) {
/* function will calculate the sum from the permutation
that is passed to it.*/
}
public boolean check_observation_2( Vector layout ) {
/* this function will check to see if all the vertices in
the graph meet the following condition as stated in observation 2:
For a set of vertices nx...ny, if nx and ny are connected by an
edge and every vertex between is connected by an edge of length
one to the vertices adjacent to it, then there is no furthur
optimization possible on this set of vertices. */
}
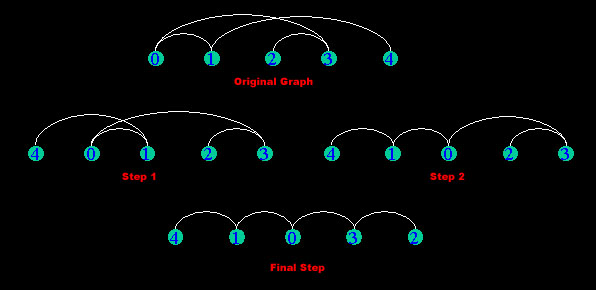
- The algorithm starts with the original graph G and creates a vector
called "vertices" which is the numerical representation of the graph.
The vector for this graph looks like this: [[1,3], [0,4], [3], [0,2], [1]]. - Next it calls the function getNextPermutation() to get a layout for the graph. In this case, [0,1,2,3,4] as can be seen in the original graph.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. If it is smaller than the current minimum sum, then it will set it to the new calculated sum. Also, the vector layout will save the current permutation layout. In this case the sum is 8 and there was no previous sum, so it sets min_sum to 8. The min_sum doesn't equal n-1, where n is the number of vertices and observation 2 is false, so the min_sum_found flag isn't set true because it didn't meet one of the stopping conditions and there are still other permutations to try.
- The while loop cycles back through and a new layout is generated by the getNextPermutation() function. For this example the new layout is [4,0,1,2,3] as can be seen in step 1.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. In this case the sum is 7, which is smaller than the previous sum of 8, so it sets min_sum to 7. The min_sum doesn't equal n-1, where n is the number of vertices and observation 2 is false, so the min_sum_found flag isn't set true because it didn't meet one of the stopping conditions and there are still other permutations to try.
- The while loop cycles back through and a new layout is generated by the getNextPermutation() function. For this example the new layout is [4,1,0,2,3] as can be seen in step 2.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. In this case the sum is 5, which is smaller than the previous sum of 7, so it sets min_sum to 5. The min_sum doesn't equal n-1, where n is the number of vertices and observation 2 is false, so the min_sum_found flag isn't set true because it didn't meet one of the stopping conditions and there are still other permutations to try.
- The while loop cycles back through and a new layout is generated by the getNextPermutation() function. For this example the new layout is [4,1,0,3,2] as can be seen in the final step.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. In this case the sum is 4, which is smaller than the previous sum of 5, so it sets min_sum to 4. The min_sum equals n-1, where n is the number of vertices, so the min_sum_found flag is set true and the while loop condition fails because we have met one of the stopping conditions.
- Thus, the algorithm returns the result and the minimum sum is 5.
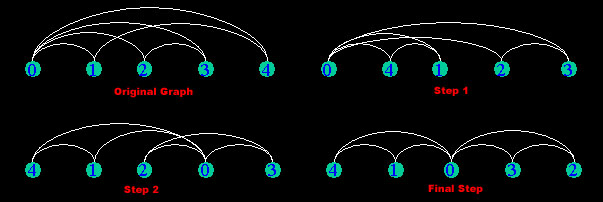
- The algorithm starts with the original graph G and creates a vector
called "vertices" which is the numerical representation of the graph.
The vector for this graph looks like this: [[1,2,3,4], [0,4], [0,3], [0,2], [0,1]]. - Next it calls the function getNextPermutation() to get a layout for the graph. In this case, [0,1,2,3,4] as can be seen in the original graph.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. If it is smaller than the current minimum sum, then it will set it to the new calculated sum. Also, the vector layout will save the current permutation layout. In this case the sum is 14 and there was no previous sum, so it sets min_sum to 14. The min_sum doesn't equal n-1, where n is the number of vertices and observation 2 is false, so the min_sum_found flag isn't set true because it didn't meet one of the stopping conditions and there are still other permutations to try.
- The while loop cycles back through and a new layout is generated by the getNextPermutation() function. For this example the new layout is [0,4,1,2,3] as can be seen in step 1.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. In this case the sum is 12, which is smaller than the previous sum of 14, so it sets min_sum to 12. The min_sum doesn't equal n-1, where n is the number of vertices and observation 2 is false, so the min_sum_found flag isn't set true because it didn't meet one of the stopping conditions and there are still other permutations to try.
- The while loop cycles back through and a new layout is generated by the getNextPermutation() function. For this example the new layout is [4,1,2,0,3] as can be seen in step 2.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. In this case the sum is 10, which is smaller than the previous sum of 12, so it sets min_sum to 10. The min_sum doesn't equal n-1, where n is the number of vertices and observation 2 is false, so the min_sum_found flag isn't set true because it didn't meet one of the stopping conditions and there are still other permutations to try.
- The while loop cycles back through and a new layout is generated by the getNextPermutation() function. For this example the new layout is [4,1,0,3,2] as can be seen in the final step.
- Now, from the permutation of the graph it calls calculate_sum to get the sum of the current layout. In this case the sum is 8, which is smaller than the previous sum of 10, so it sets min_sum to 8. The min_sum does not equal n-1, where n is the number of vertices, but observation 2 is true so the min_sum_found flag is set true and the while loop condition fails because we have met one of the stopping conditions.
- Thus, the algorithm returns the result and the minimum sum is 8.
In VLSI design, engineers need to optimize the bus system to optimize power consumption because the bus system can take up to 15%-30% of the total power in the chip. The minimum sum problem pertains in particular to bus segmentation. Bus segmentation deals with dividing the bus into several small bus segements as to reduce the power consumption as much as possible.
The bus segmentation problem can be defined as follows: Given a weighted undirected graph G = (V,E), the bus-segmentation problem is to identify a spanning tree T whose linear arrangement cost is minimum. [2]
Networks:
A polynomial-time O(log n)-approximation algorithm for finding an embedding of a network with nprocessors into an n-node linear array so as to minimize the weighted sum of the edge dilations -- i.e., for the minimum linear arrangement problem. This problem is NP-hard, and the previous best approximation bound known was O(log n log log n). In the case of planar networks, we bring the approximation factor down to O(log log n). [3]
http://www.cs.sunysb.edu/~algorith/files/bandwidth.shtml
http://www.tcs.mu-luebeck.de/AlgoDesignMan/BOOK/BOOK3/NODE137.HTM
Minimum Sum:
http://www.cs.ucr.edu/~dalton/busencode/chen.pdf
http://www.ddj.com/topics/communications/papers.htm?topic=communications
http://citeseer.nj.nec.com/cache/papers2/cs/19936/http:zSzzSzwww.dean.usma.
eduzSzmathzSzRESOURCEzSzFACULTYzSzhortonzSzsbhthesis.pdf/the-optimal-linear-arrangement.pdf
http://citeseer.nj.nec.com/cache/papers2/cs/176/http:zSzzSzwww.lsi.upc.eszSzdeptzSztechrepszSzpszSzR98-42.pdf/heuristics-for-the-minla.pdf
[2] J.Y. Chen Segmented Bus Design For Low Powered Systems, http://www.cs.ucr.edu/~dalton/busencode/chen.pdf
[3] Andrea Werneck Richa On Distributed Network Resouce Allocation, http://www.ddj.com/topics/communications/papers.htm?topic=communications